Syntax Trees for Mathematical Expressions
I got bored on Saturday afternoon so I decided to sit down and write a program that would use a neural network to automatically organize my video collection, renaming files with names like The.Conversation.1974.720p.BluRay.x264-AMiABLE [PublicHD] to something more readable like The Conversation (1974). This is my life…
Anyway, I didn't (still don't) know much of anything about neural networks, so I read some words about them and about genetic algorithms. In doing so, I ended up completing this exercise that uses a genetic algorithm to find a sequence of digits and operators that yields a certain target number. The problem I had was that his examples all parsed the sequences from left to right, ignoring order of operations (e.g. 6+5*4/2+1 = 23 instead of 17). I thought it would be fun to try to actually get the right result from these expressions, so I set out to write a simple parser for them.
What I ended up figuring out was that I could use syntax trees to represent these expressions. The easiest way to explain is with some figures, so here:
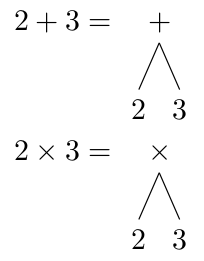
For simple expressions like 2 + 3 or 2 * 3, you get trees with just a root node (+ and * in these examples) and two leaves (the numbers). To evaluate these trees, we just evaluate each node by performing its operation on the values of its children. For a simple trees like these, we know the values of the numbers already, so we just have to perform the node operation (addition or multiplication in the examples).
More complex expressions result in more complicated trees. Order of operations is reflected in the trees by the relationships between the nodes. Since the trees end up being evaluated from the bottom up, operations that need to happen first are found nearer to the bottom of the tree. For example, for the expression 2 + 3 * 4, we get this tree:
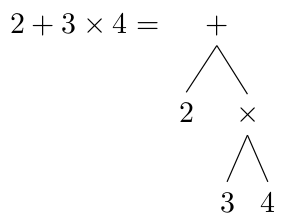
To evaluate it, we start with the + node at the top. We already know the value of the left child, 2, so we move on to the right child. This node is an operation, so we repeat the process to get its value before proceeding with the evaluation of the + node. We know the values of both of the children of this * node, so we can calculate its value by multiplying them (in this case we get 12). Now we can finish evaluating the top node, which gives us the right answer, 14, and not 20, the answer we would have gotten if we had simply evaluated from left to right.
A parser that can do this works fine for simple expressions, but it will have some problems when parentheses are used. Parentheses change the syntax of the expression by basically introducing sub-trees at specific points in the larger syntax tree. Again, this is best shown with an example.
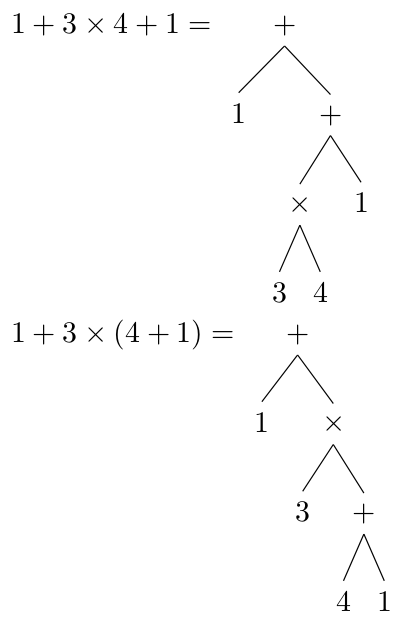
The only difference between these two expressions is the presence of parentheses, but the resulting trees are significantly different. Without parentheses, normal order of operations governs the structure of the tree, requiring the evaluation of the multiplication before the additions can be performed. With the parentheses, we can see that there is an addition that must occur before we can evaluate a multiplication, something that is impossible in a normal tree.
The reason for this structure is that the parentheses introduce a sub-tree within the expression's tree. If I write the expression this way:
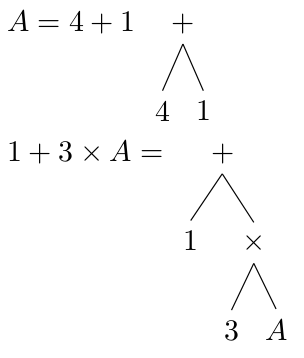
You can see that the parentheses can be parsed separately and simply inserted into the overall syntax tree at the correct position. This is what the parser I wrote does: it recursively parses whatever expression you give it, treating each set of parentheses as a separate expression to be parsed. For example, with nested parentheses, we can get structures like this:
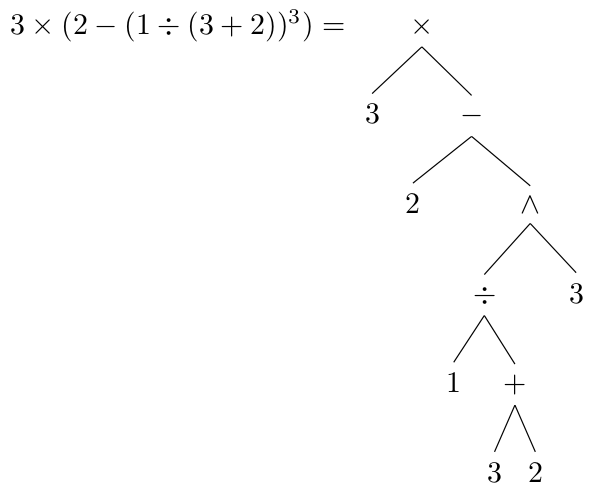
The inner-most set of parentheses (3 + 2) has to be evaluated first, then the next outer-most, and so on. Recursively parsing the tree is the best way I could think of to get this behavior and it turned out to be really simple to do in python. I put the code I wrote up on GitHub, so any more updates to it will end up there: https://github.com/PeterBeard/math-trees. You can use the code like this:
import expressionparse
t = expressionparse.Tree()
t.parse("3*(2-(1/(3+2))^3)")
print t
print t.evaluate()
This code will output the tree: [ 3 * [ 2 - [ [ 1 / [ 3 + 2 ] ] ^ 3 ] ] ] and its value, 5.976.
The library already supports variables, but it doesn't do anything with them yet. I think I'll keep working on this until it can perform tree transformations like factoring, which should eventually allow it to analytically solve (or at least simplify) algebraic expressions, and I think that would be pretty neat. Any feedback is helpful, especially if you can make the code I've written so far give an incorrect result.